Tekstopgaver, er en central del af matematikundervisningen og er ofte en udfordring for elever på alle klassetrin. Disse opgaver kræver ikke kun aritmetiske færdigheder, men også en forståelse af matematiske sammenhænge og evnen til at uddrage og anvende relevant information fra tekster.
1. Læs problemet
2. Fremhæv nøgleord og vigtige tal
3. Strukturer informationen
4. Formuler ligningen
(5. Visualiser problemet)
6. Udfør beregningen
7. Kontrollér resultatet
At løse tekstproblemer kræver en systematisk tilgang og strategisk tænkning. I denne artikel vil vi præsentere forskellige metoder og tips, der kan hjælpe dig med at løse tekstproblemer mere effektivt. Fra grundlæggende strategier for yngre elever i grundskolen til mere sofistikerede metoder for ældre elever, der forbereder sig til indplaceringstest og komplekse matematikopgaver, giver denne guide værdifuld indsigt og øvelser.
Ved at guide dem gennem eksempler og påpege almindelige fejlkilder ønsker vi at give eleverne de værktøjer, de har brug for til at mestre matematiske problemer med selvtillid og kompetence og udvide deres generelle matematiske viden.
Hvad er tekstopgaver, og hvorfor bliver de stillet? 🤔
Tekstopgaver, ofte omtalt som faktuelle opgaver i grundskolen, er matematikopgaver, der præsenteres i form af tekster. De kræver mere end blot at anvende aritmetiske operationer; eleverne skal forstå teksten, filtrere de relevante informationer og udvikle en matematisk løsning på dette grundlag. I modsætning til rene aritmetiske opgaver, som fokuserer på tal og ligninger, afspejler tekstopgaver problemer fra den virkelige verden og kræver anvendelse af matematik i praktiske situationer.
Hovedformålet med tekstproblemer er at forbedre problemløsningsfærdigheder. De hjælper eleverne med at udvikle kritisk tænkning og analytiske færdigheder ved at lære at afkode komplekse oplysninger og omsætte dem til matematiske ligninger. Tekstopgaver træner elevernes forståelse af matematiske begreber og forbereder dem på at anvende denne viden i hverdagsscenarier, som f.eks. beregning af omkostninger, tidsstyring eller videnskabelige projekter.
Ved at integrere disse opgaver i matematiktimerne opfordres eleverne til at tænke ud over simpel aritmetik og se matematik som et nyttigt værktøj til forskellige udfordringer i livet. Find region Nordjylland matematik lektioner til dig, der bor i regionen.
Tips til at løse tekstproblemer 💡
At løse tekstproblemer kan ofte være en hovedpine for studerende. Men med en systematisk tilgang og de rigtige teknikker kan selv komplekse tekstproblemer løses effektivt.
Trin-for-trin-guide til systematisk løsning:
- Læs opgaven grundigt: Tag dig tid til at læse tekstopgaven grundigt. Prøv at forstå essensen af opgaven, og hvad der præcist kræves. Det er det første skridt til at sikre, at du får alle de nødvendige oplysninger med.
- Fremhæv nøgleord og tal: Identificer og fremhæv alle vigtige tal og nøgleord i teksten, som indikerer, hvilke matematiske operationer der er nødvendige. Ord som "sammen", "fjern", "mere end" eller "resterende" kan indikere, om du skal addere, subtrahere, multiplicere eller dividere.
- Strukturer information: Skriv ned, hvad der er givet, og hvad der søges efter. At lave en liste over de givne data og den løsning, du leder efter, hjælper dig med at strukturere opgaven.
- Formuler ligningen: Baseret på de oplysninger, du har indsamlet, skal du formulere en eller flere ligninger. Dette trin er afgørende, da det oversætter dine tanker fra teksten til matematikkens sprog.
- Visualiser problemer: Nogle gange hjælper det at lave et diagram, en tegning eller en tabel for bedre at kunne visualisere problemet og forstå forholdet mellem dataene.
- Beregn: Løs ligningerne ved hjælp af skrevne beregninger med de fremhævede oplysninger. Sørg for at udføre hvert beregningstrin omhyggeligt for at undgå fejl.
- Tjek resultatet: Når du har fundet et svar, skal du læse opgaven igennem igen og tjekke, om dit resultat giver mening og er korrekt. Sørg for, at du har besvaret alle dele af spørgsmålet.
At øve sig er nøglen til at mestre matematiske problemer. Brug øvelser fra din matematikbog eller online-ressourcer til at skærpe dine færdigheder. Regelmæssig brug af disse teknikker vil forbedre din forståelse og evne til at løse tekstproblemer betydeligt.
Beregningseksempler for forskellige klasser 🟰
Grundskole (2. klasse):
Addition og subtraktion
Opgave 1: Tim har 5 kr. og finder 3 kr. på legepladsen. Hvor mange penge har Tim nu?
- Beregning: 5 kr. + 3 kr. = 8 kr.
- Svar: Tim har nu 8 kr.
Opgave 2: Anna har 8 stykker slik. Hun giver sin veninde 3 bolsjer. Hvor mange bolsjer har Anna tilbage?
- Rechnung: 8 bolsjer - 3 bolsjer = 5 bolsjer.
- Antwort: Anna har nu 5 bolsjer tilbage.
Mellemniveau (5. og 6. klasse):
Multiplikation, division, omregning af enheder og simple brøker
Opgave 3: En klasse med 24 elever er ved at planlægge en udflugt. Hvert barn må tage 500 ml vand med. Hvor mange liter vand er det i alt?
- Beregning: 24 børn × 500 ml = 12000 ml = 12 liter
- Svar: Eleverne tager i alt 12 liter vand med sig.
Opgave 4: På en gård er 56 æbler jævnt fordelt på 8 kasser. Hvor mange æbler er der i hver kasse?
- Beregning: 56 æbler ÷ 8 kasser = 7 æbler pr. kasse
- Svar: Der er 7 æbler i hver kasse.
Overbygningen (fra 7. klasse):
Kombination af forskellige matematiske operationer, anvendelse af procentregning og geometri. Uanset dit niveau kan du finde matematik b kursus København.
Opgave 5: En rektangulær mark har en længde på 150 meter og en bredde på 80 meter. Hele marken skal omkranses af et hegn. Hvor mange meter hegn er der brug for?
- Beregning: (150 m + 80 m) × 2 = 460 m
- Svar: Der er brug for 460 meter hegn.
Opgave 6: En butik sælger en cykel, der oprindeligt koster 400 euro, med en rabat på 15 %. Hvor meget koster cyklen efter rabatten?
- Faktura: 400 euro × 15 % = 60 euro; 400 euro - 60 euro = 340 euro.
- Svar: Cyklen koster 340 euro efter rabatten.
Klasse 8 og 9:
Procentberegning, tredeling og indirekte proportionalitet
Opgave 7: Et skib har forsyninger nok til 40 dage til en besætning på 15 personer. Find matematik undervisning online eller fysisk på Superprof!
Del a: Hvor mange dage kan forsyningerne række, hvis der kun er 8 besætningsmedlemmer om bord?
- Beregning: 40 dage x (15/8 mennesker) = 75 dage
- Svar: Forsyningerne rækker til 75 dage, hvis der kun er 8 personer om bord.
Del b: Hvor mange mennesker vil der være nok forsyninger til, hvis skibet sejler i 30 dage?
- Beregning: 15 mennesker x (40/30 dage) = 20 personer
- Svar: Forsyningerne rækker til 20 personer, hvis skibet skal sejle i 30 dage.
Del c: Hvor mange dage kan provianten række, hvis 5 mænd og 1 kvinde går om bord på skibet efter 28 dage, og kvinden bruger en tredjedel mindre proviant pr. dag end en mand?
- Beregning: Samlet forbrug pr. dag efter 28 dage: (2 personer / (3+5 mænd)) = 5 + (2/3 resterende forsyninger) : 12 dage x15 personer= 180 persondage; ny varighed: 180 persondage / (5+(2/3mennesker)) = 31,7 dage.
- Svar: Efter de første 28 dage kan skibet blive på havet i yderligere ca. 32 dage.
Opgave 8: Malte og Nele har samlet 4 kg friske svampe, som består af 95 % vand og 5 % tørstof.
Del a: Hvor mange kilo vand og tørstof indeholder de 4 kg friske svampe?
- Beregning: Vand: 4 kg×95 %=3,8 kg; Tørstof: 4 kg x 5 % = 0,2 kg.
- Svar: De friske svampe indeholder 3,8 kg vand og 0,2 kg tørstof.
Del b: Hvor mange kg vand og tørstof indeholder disse svampe efter tørring, hvis de kun består af 80 % vand?
- Beregning: Ny vandmasse, som svarer til 80 % af den samlede masse efter tørring. Den tørre masse er stadig 0,2 kg, så den samlede masse x 80 % = 1 kg, vand: 1 kg - 0,2 kg = 0,8 kg.
- Svar: Efter tørring indeholder svampene 0,8 kg vand og 0,2 kg tørstof.
Del c: Hvor stor en procentdel af svampens masse går tabt under tørringen?
- Beregning: Massetab: 4 kg - 1 kg=3 kg; Procentvis tab:
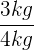x 100 % = 75 %. - Svar: 75 % af svampens masse går tabt under tørringen.
Disse eksempler illustrerer, hvordan matematikopgaver varierer efter klassetrin for at støtte børns voksende forståelse og færdigheder. I indskolingen er der fokus på grundlæggende talforståelse og simpel aritmetik. På mellemtrinnet bliver opgaverne mere komplekse med introduktion af store tal, måleenheder og forholdstal, mens der i udskolingen øves brug af avanceret aritmetik og løsning af opgaver, der kræver flere trin.
Almindelige fejl og misforståelser 💥
Når man løser tekst- og faktaproblemer i matematik, opstår der ofte typiske fejl, som normalt skyldes misforståelser af teksten eller de matematiske procedurer. En almindelig fejl er at overse vigtig information i teksten, hvilket ofte sker, når studerende ikke læser opgaven grundigt. For at undgå dette er det vigtigt at læse tekstopgaven omhyggeligt flere gange og at fremhæve nøgleord og tal, der er afgørende for at løse opgaven.
Det er dog også muligt, at flere oplysninger og tal end nødvendigt bevidst er medtaget i tekstopgaven. Du bør derfor altid spørge dig selv: "Hvad er ønsket?" og "Hvad er givet?" for kun at markere de oplysninger, der er relevante for opgaven. Bliv bedre til matematik med matematik hjælp.
En anden fejl er forkert anvendelse af matematiske operationer. Eleverne kan undgå dette ved at kontrollere hvert trin i udregningen og spørge sig selv, om den valgte operation virkelig fører til det ønskede resultat. Regelmæssig øvelse af matematiske problemer og deltagelse i øvelser, der uddyber forståelsen, er afgørende her.
For at minimere fejl bør resultatet kontrolleres kritisk efter hver afsluttet opgave. Sørg for, at svaret er logisk og giver mening i opgavens sammenhæng. Dette trin hjælper ikke kun med at genkende fejl, men fremmer også en dybere forståelse af de matematiske begreber bag opgaverne. Find matematik lektiehjælp Århus, Aalborg og i alle andre danske byer, så du kan komme tættere på dine mål!
Kunne du lide denne artikel? Skriv en anmeldelse!
Loading...
