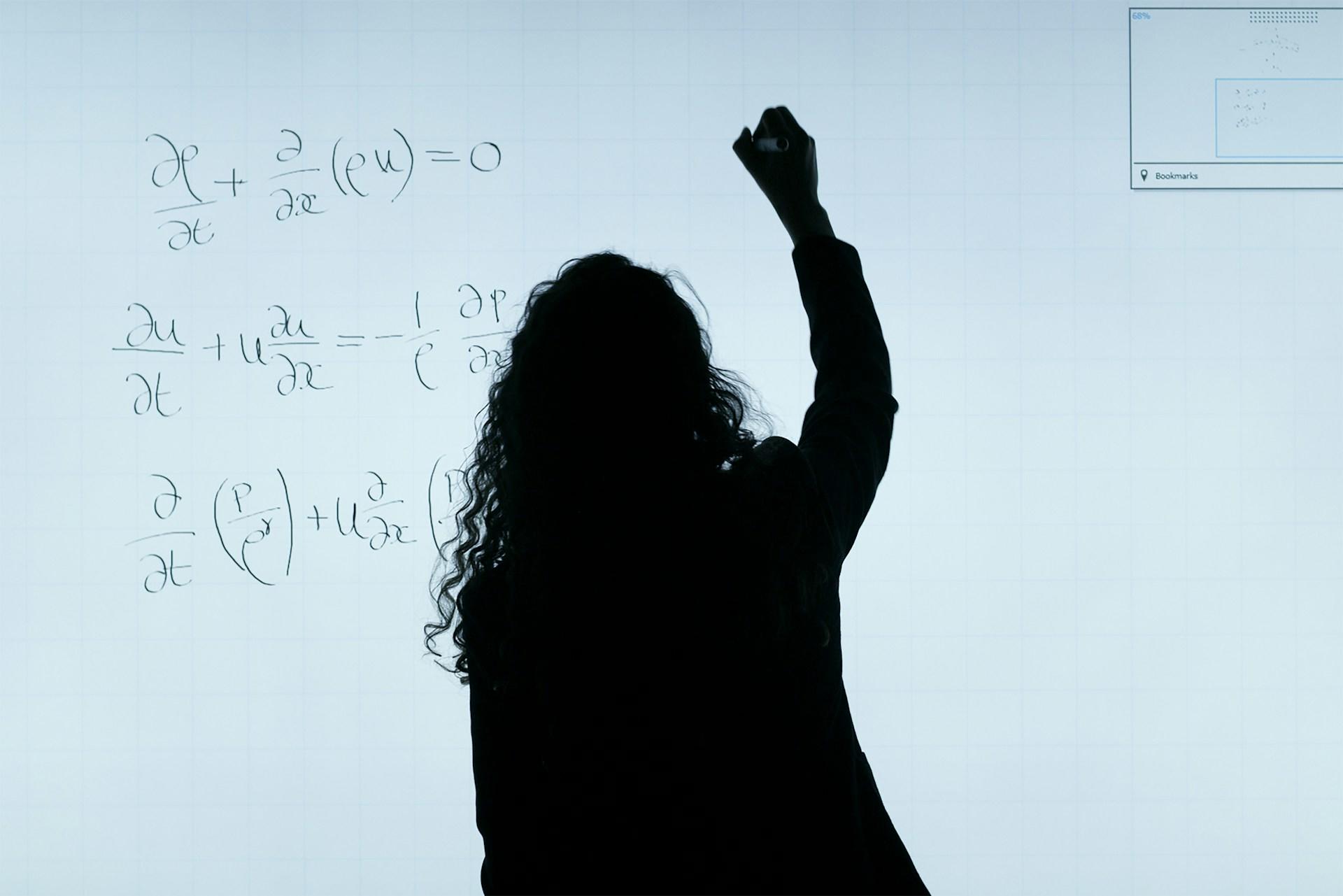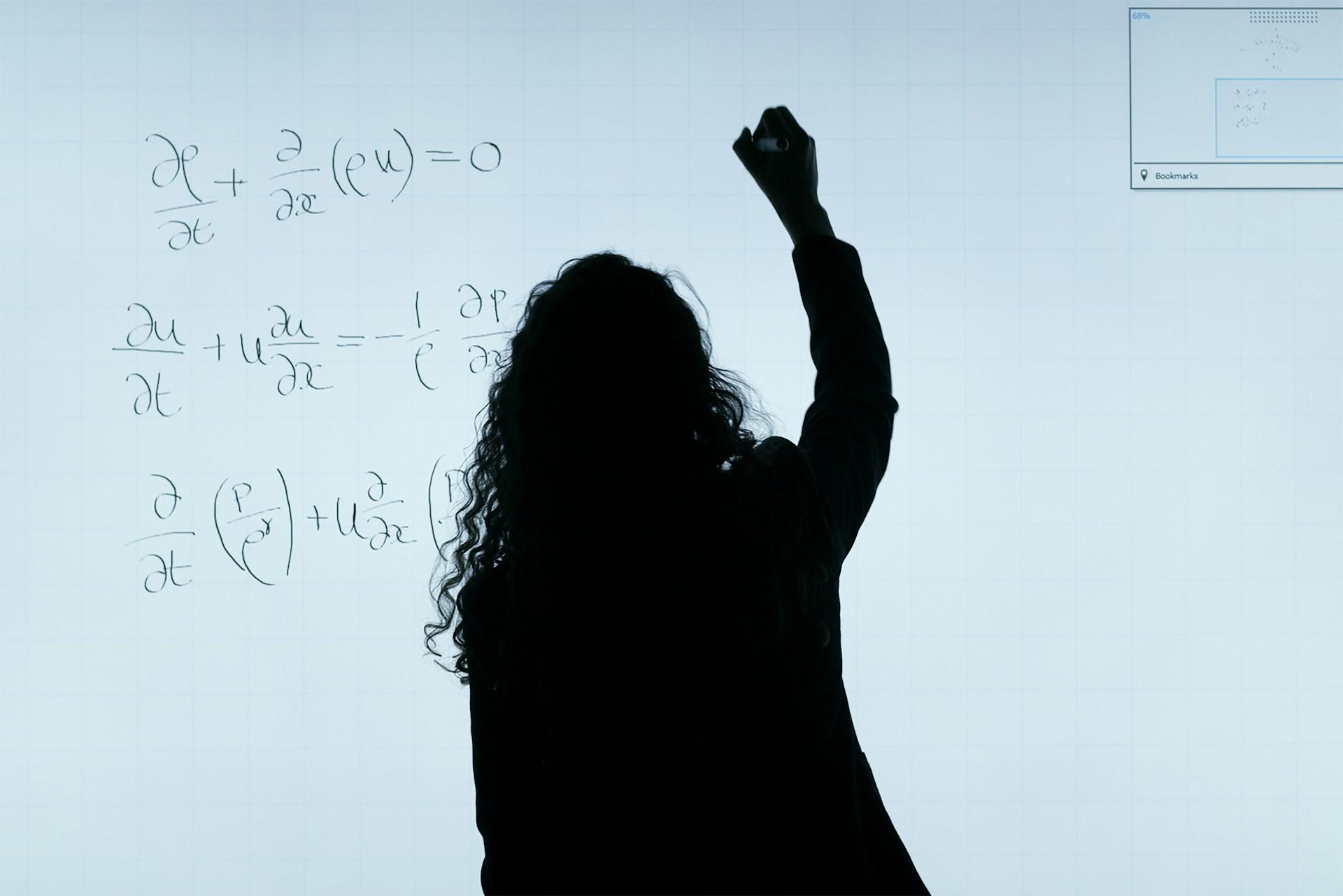Ved at studere matematik kan du først og fremmest forvente at udvikle en række nøglefærdigheder, som er efterspurgte af arbejdsgivere, og som også vil hjælpe dig i dit daglige liv. For eksempel opmuntrer matematik til logisk tænkning, beslutningstagning og problemløsning, som alle er afgørende for at overleve i det moderne samfund.
Dertil kommer, at matematik er et vigtigt studieområde for dem, der søger en karriere inden for finans-, ingeniør- og informationsteknologi. Nogle af de job, der er direkte relateret til en matematisk uddannelse, er statsautoriseret revisor, investeringsanalytiker, systemudvikler og gymnasielærer i matematik, som alle omfatter brug af matematiske begreber som dem, vi vil se på nedenfor.
Overvejelser ved valg af matematik på A-niveau
Når man overvejer at vælge Matematik på A-niveau, er det vigtigt at være opmærksom på, at faget stiller høje krav til både arbejdsindsats og abstrakt tænkning.
Niveauet indebærer en betydelig udvidelse i forhold til B-niveau, både i pensum og i det teoretiske dybdeniveau. Man arbejder med avancerede emner som differential- og integralregning, vektorregning, sandsynlighedsteori og matematisk modellering.
Det kræver en vis tryghed ved algebra, funktioner og symbolsk notation, samt villighed til at bruge tid på lektier, opgaveregning og forståelse af beviser og begreber.
Til gengæld giver Matematik A adgang til mange videregående uddannelser inden for naturvidenskab, teknik, økonomi og sundhed. Derfor er det et godt valg for elever, der har interesse for faget og kan lide at løse logiske problemer – men det er også et fag, der kræver vedholdenhed og disciplin.
De overordnede temaer i matematik på A-niveau
Når man vælger matematik på A-niveau i gymnasiet, træder man ind i et fag, der både er teoretisk og praktisk, abstrakt og konkret.
De overordnede temaer spænder bredt og inkluderer blandt andet:
- funktioner
- differential- og integralregning
- vektorregning
- statistik
- sandsynlighedsregning
- matematiske beviser
Centralt i undervisningen er arbejdet med at modellere virkelige fænomener – fx vækst, bevægelse eller usikkerhed – ved hjælp af matematiske begreber og værktøjer.
Der lægges stor vægt på både analytisk tænkning og præcision i argumentation, og faget kombinerer kreative strategier med logisk struktur. Det er et fag, hvor man lærer at tænke skarpt, se mønstre og finde løsninger – og hvor matematikken bliver et sprog til at forstå verden.
Lad os se nærmere på nogle af temaerne som man skal lære på matematik A-niveau.
Differential- og integralregning
Differentiering er et matematisk værktøj, der primært bruges til at beregne ændringshastigheder. Værktøjet giver os således mulighed for at finde hastighedsændringen i forhold til tiden (dvs. acceleration) samt ændringshastigheden for x i forhold til 'y' på en graf (dvs. kurvens hældning).
Som en del af matematik på A-niveau, vil din lærer uden tvivl lære dig de grundlæggende regler for differentiering.
Det vil du for eksempel lære:
Hvis y = en funktion af x (et udtryk, der indeholder x'er og tal), så skrives den afledte funktion af y i forhold til x dy/dx.
Ud over ovenstående simple regel vil du næsten helt sikkert lære om 'Differentiering af x i potens af noget', at bringe potensen ned foran x og derefter reducere potensen med en.
Sammen med denne potensregel er andre underliggende temaer inden for eksplicit differentialregning:
- konstantreglen
- konstantmultipelreglen
- sumreglen
- differensreglen.
Differentiering handler, som nævnt ovenfor, om kurver og gradienter, og derfor vil du ved hjælp af al den ovenstående viden i sidste ende kunne differentiere ligningen for en kurve og finde en formel for dens gradient.
Hvis alt dette lyder lidt forvirrende, kan du være sikker på, at din matematiklærer vil være i stand til at forklare processerne og funktionerne, så de bliver lette at forstå for dig.
En privatlærer vil også kunne hjælpe dig med at forstå hvad logaritmer er og hvordan de anvendes.
Vektorregning
Vektorregning er en central del af matematikundervisningen på A-niveau i gymnasiet. Det handler om at arbejde med vektorer – størrelser, der både har en retning og en længde.
Vektorregning bruges til at beskrive og analysere geometriske og fysiske problemstillinger, f.eks. bevægelser, kræfter og positioner i planen eller rummet. På A-niveau lærer man at regne med vektorer i både to og tre dimensioner, herunder
- addition
- subtraktion
- skalar multiplikation
- beregning af længde
Man arbejder også med begreber som skalarprodukt (prikprodukt), vektorprojektioner og vinkler mellem vektorer, som alle har vigtige anvendelser i både matematik og naturvidenskab. Desuden lærer man at bruge vektorer til at opstille ligninger for linjer og planer samt til at løse geometriske problemer analytisk.
Vektorregning giver dermed både et værktøj til abstrakt tænkning og en praktisk metode til at løse konkrete problemer.
Statistik
Statistik handler om at indsamle, analysere og tolke data for at sige noget meningsfuldt om virkeligheden.
I gymnasiet lærer man at arbejde med forskellige statistiske begreber som:
- middelværdi
- median
- spredning
- standardafvigelse
Man bruger grafer og tabeller til at få overblik over data, og man undersøger, om der er sammenhænge mellem forskellige variabler.
Et centralt element er også sandsynlighed, hvor man vurderer, hvor sandsynligt det er, at noget sker.
Statistikken bruges ofte i samfundsmæssige og naturvidenskabelige sammenhænge – fx til at analysere spørgeskemadata, tolke sundhedstal eller forudsige udviklinger.
Eleverne lærer ikke bare at regne på tallene, men også at stille kritiske spørgsmål: Hvad viser dataene – og hvad viser de ikke?
Matematiske beviser
I matematik handler det ikke kun om at finde det rigtige svar – det handler også om at forstå, hvorfor det er rigtigt. Det er her matematiske beviser kommer ind i billedet. Et bevis er en logisk og trinvis forklaring, der viser, at en påstand altid gælder, uanset hvilke tal eller figurer man arbejder med. I gymnasiet er arbejdet med beviser en central del af A-niveauet, fordi det skærper den matematiske forståelse og træner evnen til at tænke systematisk og præcist.
Et klassisk eksempel på et bevis, som mange møder tidligt, er Pythagoras’ sætning: I en retvinklet trekant gælder det, at kvadratet på hypotenusen er lig summen af kvadraterne på de to kateter, altså a2+b2=c2a^2 + b^2 = c^2a2+b2=c2.
Her lærer eleverne ikke blot at bruge sætningen til at beregne længder, men også at bevise, hvorfor den gælder – fx ved hjælp af geometriske figurer eller algebraiske omformninger.
Et andet eksempel kan være beviset for, at kvadratroden af 2 er et irrationelt tal – et modstridsbevis, hvor man antager det modsatte og når frem til en logisk umulighed.
Man arbejder også med beviser i funktionsteori, f.eks. at hvis en funktion er differentiabel i et punkt, så er den også kontinuert dér.
Eller man bruger matematisk induktion til at bevise, at en formel gælder for alle naturlige tal, som fx summen af de første nnn ulige tal.
Gennem arbejdet med beviser lærer man at argumentere klart og logisk, og man opbygger en mere dybtgående forståelse af det matematiske system som helhed. Det er ikke altid nemt – men det er netop derfor, det er så værdifuldt.
Karrieremuligheder med fokus på matematik
En stærk matematisk baggrund åbner dørene til mange spændende og alsidige karrierer. Matematik er grundlaget for en lang række fagområder, og derfor er der stor efterspørgsel på mennesker med gode matematiske kompetencer.
Man kan f.eks. arbejde som
- ingeniør
- økonom
- dataanalytiker
- aktuar
- softwareudvikler
- statistiker
Inden for naturvidenskab og teknologi bruges matematik til forskning, modellering og problemløsning, mens det i samfundsvidenskabelige og erhvervsøkonomiske sammenhænge bruges til analyse, prognoser og beslutningsstøtte.
Matematik spiller også en vigtig rolle i den finansielle sektor, inden for kunstig intelligens, maskinlæring og kryptologi.
Desuden kan man undervise i matematik på forskellige niveauer eller arbejde med formidling og forskning.
Kort sagt: Matematik giver ikke blot tekniske færdigheder, men også evnen til at tænke kritisk og struktureret – noget der værdsættes i mange typer jobs.
Få styr på matematikken med en privatunderviser
Matematik på A-niveau kan være udfordrende – både fordi stoffet er komplekst, og fordi tempoet i undervisningen ofte er højt. Du skal for eksempel lære om infinitesimalregning, geometri, statistik og meget mere. Hvis man sidder tilbage med spørgsmål, manglende forståelse eller bare har brug for at få tingene forklaret på en anden måde, kan en privat tutor være en rigtig god investering.
En tutor kan tage udgangspunkt i netop dine behov, forklare emner i dit tempo og give konkrete redskaber til både opgaver og eksamen. Det kan øge både faglig forståelse og selvtillid – og i mange tilfælde gøre en mærkbar forskel på karakteren.
Der findes flere steder, hvor man kan finde dygtige og erfarne undervisere, og Superprof er en af de mest populære platforme i Danmark. Her kan man søge efter matematikundervisere i sit område eller online, læse anmeldelser fra tidligere elever og finde en tutor, der passer til ens niveau og læringsstil.
Uanset om du kæmper med differentialregning eller har brug for hjælp til statistik og beviser, kan en god tutor gøre matematikken både mere forståelig og mere overkommelig.
Kunne du lide denne artikel? Skriv en anmeldelse!
Loading...
