Velkommen til en udforskning af et grundlæggende koncept i matematik, som ofte forbliver indhyllet i mystik for mange: lovene om logaritmer.
For dem, der vover sig ind i matematikken og kalkulationen, kan funktionen af en lommeregnerknap med betegnelsen "log" være velkendt. I dag ser vi nærmere på logfunktionen med nogle enkle definitioner af logaritmerne og eksempler på, hvordan de bruges.
Dette bliver endnu et algebra-tungt emne, så hvis du ikke allerede er fortrolig med at arbejde med algebra, er det måske bedst at genopfriske det først og så komme tilbage hertil.
Logaritmernes love er et sæt regler, der hjælper med at forenkle og manipulere logaritmiske udtryk. Disse love giver retningslinjer for at kombinere, opdele og evaluere logaritmer, hvilket gør det lettere at løse komplekse ligninger, der involverer logaritmefunktioner.
I løbet af din uddannelse vil du finde logaritmer mest nyttige, når du løser eksponentielle ligninger, og du vil se hvorfor nedenfor!
Lad os gå i gang med at se på nogle af logaritmelovene, og hvordan du kan bruge dem i praksis til at løse svære spørgsmål.
Den eksponentielle funktion
Lad os få et specialtilfælde af vejen først. Du er sikkert allerede stødt på eksponentialfunktionen, den skrives ganske enkelt med notation som "ex", og du ser den måske i et udtryk som dette:
En eksponent er det modsatte af en logaritme.
Hvis du ikke er så bekendt med eksponenter, har de en særlig egenskab, som gør dem nyttige. Den afledte af "e" (som er en forkortelse for "eksponentiel form") er lig med sig selv, det vil sige, at hvis vi skulle differentiere (lær mere om differentiering/integrationsproblemer her) udtrykket ovenfor, ville vi ende med følgende:
Den afledte af eksponenten.
Når vi bruger logaritmer (også kendt som logaritmiske funktioner), bruger vi typisk "ln"-notationen til at repræsentere det, der kaldes den "naturlige log" - det er den omvendte funktion af eksponenten.
Hvad er eksponenten helt præcist? Det er det, man kalder en "konstant", fordi den aldrig ændrer sig. "e" repræsenterer et specifikt reelt tal med mange decimaler, så det er lettere bare at repræsentere det ved hjælp af en almindelig notation som et enkelt bogstav. Ligesom vi gør med Pi!
Før vi går i gang med at se nærmere på logaritmereglerne, skal vi lave et hurtigt eksempel på et spørgsmål, der bruger naturlige logaritmer.
Eksempel på naturlig logaritme
Her er et eksempel på et spørgsmål:
For eksponentialligningen nedenfor skal du løse for x:
Umiddelbart ser det svært ud, men det er kun, fordi vi har et "e" (eksponentiel) med i blandingen. Jeg tror, vi alle kan blive enige om, at når det først er ude af billedet, bliver det hele meget nemmere. Men hvordan gør man det?
Heldigvis har "ln" en anden praktisk egenskab: Det er det omvendte af "e", hvilket betyder, at vi ved at tilføje det til vores ligning kan ophæve eksponentialet - ligesom man kan dividere en ligning med et tal for at slippe af med en koefficient.
Lad os gøre det nu:
Husk, at med ligninger skal alt, hvad vi gør på den ene side af ligningen, også gøres på den anden. Nu vil "ln" og "e" ophæve hinanden, ligesom når man ganger og derefter dividerer med det samme tal.
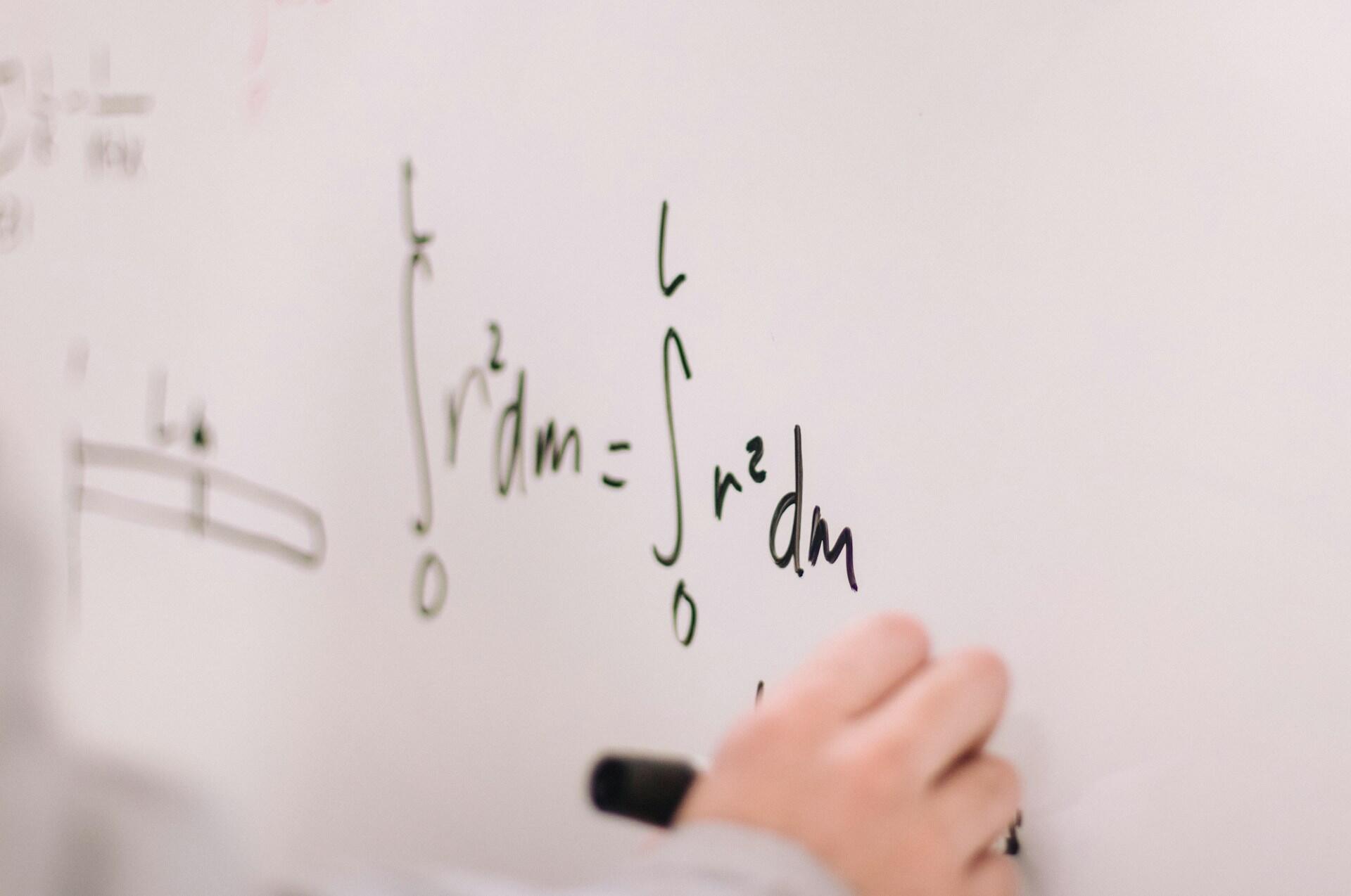
Når det er afklaret, har vi vores svar:
Vores eksponentielle ligning er nu løst! Vi behøver ikke at gøre mere med ln(...), da dette repræsenterer et reelt tal - sæt det ind i en hvilken som helst grafisk eller videnskabelig lommeregner og se!
Er du blevet nysgerrig på at finde ud af hvordan du kan løse matematikopgaver til analytisk mekanik?
Lovene for logaritmer
Der er noget, man skal huske på, når man ser på logaritmelove - i alle eksemplerne nedenfor bruger vi bare "loga", den notation, der normalt bruges med logaritmer, er enten "log", når logaritmefunktionen bruger base10, eller "loga", hvor "a" er et tal, når logaritmen bruger en anden base.
Enhver lov kan anvendes på ethvert basissystem, forudsat at der ikke er nogen ændring af basen i udtrykket. For eksempel gælder alle disse love også for base3-tal, så længe du bruger base3 for hvert tal i dit udtryk.
Loglov 1: Loven om produkt (addition)
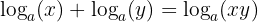
Denne lov bruger additions- og multiplikationsegenskaber.
Den første lov siger, at det at lægge logaritmerne af to tal (med samme basis!) sammen er det samme som at tage logaritmen, efter at vi har ganget tallene sammen.
Logaritmisk lov 2: Kvotientloven
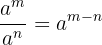
Denne lov bruger divisions- og subtraktionsegenskaber.
Den anden lov siger, at subtraktion af logaritmerne af to tal (igen med samme base) svarer til at dividere de to tal og tage logaritmen af resultatet.
Logaritmelov 3: Potensloven
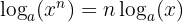
Denne logaritmelov bruger eksponentens egenskaber.
Den sidste logaritmelov, vi ser på, virker måske bekendt for dig - den minder meget om at differentiere et udtryk! Logaritmen af et tal opløftet til en potens er det samme som at gange hele logaritmen med eksponenten og dermed fjerne eksponenten fra det oprindelige udtryk.
Loglov 4: Ændring af grundloven
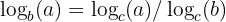
Denne lov giver dig mulighed for at konvertere en logaritme fra en base til en anden.
Loven om ændring af basislogaritmer er særlig nyttig, fordi lommeregnere typisk kun har knapper til logaritmer i basis 10 (almindelige logaritmer, betegnet som log) og basis e (naturlige logaritmer, betegnet som ln), men du kan støde på logaritmer i andre baser i forskellige matematiske problemer.
Oversigtstabel: De 7 love for logaritmer
| Reglens navn | Log regel ligning | Forklaring |
|---|---|---|
| Produkt-regel |  | Logaritmen af et produkt er summen af logaritmerne. |
| Kvotient-regel |  | Logaritmen af en kvotient er forskellen mellem logaritmerne. |
| Potens-regel |  | Logaritmen af en potens er eksponenten gange logaritmen. |
| Regel om ændring af basis |  | Gør det muligt at ændre basen for en logaritme til en anden base. |
| Nul-eksponent-regel |  | Logaritmen af 1 er altid 0, uanset basen. |
| Log af 1 |  | Logaritmen af basen til sig selv er altid 1. |
| Log af basen |  | Basen hævet til logaritmen af et tal giver tallet. |
Sådan løser du logaritmiske ligninger
Logaritmerne ser isoleret set ret enkle ud, men desværre er det sjældent så let til eksamen. Normalt vil du blive stillet over for udsigten til at skulle bruge et vilkårligt antal kombinationer af logaritmefunktioner for at komme frem til et svar.
Det kan virke skræmmende i starten, men som altid er den bedste måde at nærme sig disse problemer på at tackle dem i små bidder: at dele spørgsmålet op i mindre problemer. Dette gør sig i øvrigt gældende for de fleste matematiske opgaver.
Løsning af logaritmiske ligninger involverer anvendelse af logaritmernes egenskaber og algebraisk manipulation. Her er en trin-for-trin-guide:
Trin 1: Evaluer logaritmer
Hvis den ukendte variabel er uden for logaritmen, skal du bruge logaritmens base til at evaluere selve logaritmen. Hvis du f.eks. har ( \log_b(x) = y ), kan du omskrive det til ( x = b^y ) for at løse ( x ). Dette er ligetil, når basen og argumentet for logaritmen er nemme at arbejde med, men kan kræve en lommeregner for mere komplicerede værdier.
Trin 2: Konverter til eksponentiel form
Hvis den ukendte variabel er inde i logaritmen, skal du omskrive ligningen til eksponentiel form. For eksempel, for ligningen ( \log_b(x) = y ), omskriv den som ( x = b^y ). Dette giver dig mulighed for at løse den ukendte variabel ved at hæve basen af logaritmen til potensen af den anden side af ligningen.
Trin 3: Kombiner logaritmer
Hvis der er flere logaritmer i en ligning, kan du prøve at kombinere dem ved hjælp af logaritmernes egenskaber. Du kan f.eks. kombinere to logaritmer med samme basis ved at addere eller subtrahere dem. Det kan forenkle ligningen og gøre den lettere at løse.
Trin 4: Tjek for fremmede løsninger
Når du har fundet en løsning, skal du altid tjekke den for at sikre, at den er gyldig. Nogle løsninger er måske ikke gyldige, fordi de resulterer i at tage logaritmen af et negativt tal eller nul, hvilket er udefineret. Disse kaldes uvedkommende løsninger og skal kasseres.
Trin 5: Øv algebraisk manipulation
Logaritmiske ligninger kræver ofte algebraisk manipulation såsom faktorisering, kombination af ens udtryk eller brug af eksponenternes egenskaber til at løse dem. Øv dig i disse algebraiske teknikker for at blive bedre til at løse logaritmiske ligninger.
Husk, at løsning af logaritmiske ligninger nogle gange kan indebære forsøg og fejl eller flere trin, så tålmodighed og øvelse er nøglen.
Logaritmisk lov - eksempel
Lad os undersøge log-ligningen nedenfor:
En blanding af logaritmeoperationer udgør et udtryk
Her er alle termerne i vores udtryk i base10, så vi angiver ikke en base. Spørgsmålet er, hvordan vi kan forenkle dette? Hvis du er i stand til at se det første trin, så løser alt andet sig stort set af sig selv.
Alt, hvad vi har gjort her, er at omskrive den anden logaritmefunktion ved at bruge den tredje af logaritmernes egenskaber, som vi så på ovenfor. Det giver os mulighed for at gøre det andet led i udtrykket til et polynomium. Det andet udtryk, vi er endt med (og det andet udtryk i det oprindelige spørgsmål evalueres begge ens) og er bare udtrykt på forskellige måder. Hvis du ikke tror på mig, kan du tjekke det på en lommeregner ved kun at indtaste det andet led i udtrykket.
Gør dette en gang for det udtryk, vi lige har oprettet, og en gang for det oprindelige udtryk, og du bør se, at de begge har samme værdi.
Når alt kommer til alt, er alle tal tal: Det betyder, at vi kan tage vores to i potens med tre og gøre det til 8. Lad os gøre det:
Det begynder at se bedre ud. Vi kommer tættere på bare at kunne udføre simpel aritmetik. Hvis du ikke er sikker på, hvad der nu skal ske, kan du kaste et blik på logaritmelovene, som vi beskrev tidligere, og se, om du kan finde ud af, hvor vi skal hen herfra.
Det næste skridt er at forenkle endnu mere ved at fjerne endnu et udtryk. Vi kan nu bruge den første logaritmelov, vi har lært, nemlig at det at lægge to logaritmer sammen er det samme som at gange deres numeriske udtryk. Når vi har gjort det, står vi tilbage med to logaritmer. Vi er næsten i mål!
Vi har ganget de to første tal sammen til 32 og forenklet vores udtryk til to logaritmer.
Se ovenfor, og du vil se, at der kun er én lov tilbage, som vi ikke har brugt, og forhåbentlig vil du også se, at den passer perfekt til den sidste del af vores problem! Vi kan nu trække de to logaritmer fra hinanden:
Vi kan ikke forenkle den brøk længere, så vores endelige svar bliver:
Og så er vi færdige!
Indpakning af reglerne for logaritmer
Den gode nyhed er, at lovene for logaritmer er ret enkle i sig selv - alt, hvad du behøver, er en god forståelse af grundlæggende aritmetik, og så er du godt på vej. Der, hvor det bliver sværere, er at kombinere disse love for at løse mere komplekse problemer.
Logaritmer vil sandsynligvis dukke op ofte, når du står over for beregningsspørgsmål, så sørg for, at du er fortrolig med at bruge dem.
Som altid i matematik gælder det, at øvelse gør mester! Selv om disse matematiske begreber ikke ser ud af meget i sig selv, er de alle sammen vigtige tandhjul i en stor maskine! Hvis du har lyst til nogle ekstra aktiviteter, der involverer logaritmiske ligninger og eksponentfunktioner, kan du prøve at tegne grafer over e(x) og ln(x) og se, om du kan få øje på nogle mønstre.
Hvis du har svært ved det, kan du overveje at bruge SuperProf til at finde matematiklærere, der kan give dig en hjælpende hånd til at forstå de matematiske begreber bedre. En privatunderviser kan skræddersy undervisningen for dig, så du kan arbejde med matematiske områder som infinitesimalregning, geometri, ligninger og meget mere.
Kunne du lide denne artikel? Skriv en anmeldelse!
Loading...
