Skriftlig regning er en grundlæggende færdighed i matematik, som eleverne lærer allerede i folkeskolen, og som er vigtig for elever i alle klasser. Det er en metode, der gør det muligt at løse matematiske problemer på skrift, hvad enten det drejer sig om addition, subtraktion, multiplikation eller division.
Skriftlig regning er mere end bare en teknisk proces; den fremmer logisk tænkning og problemløsningsevner. Denne artikel forklarer ikke kun i detaljer de forskellige teknikker i skriftlig aritmetik, addition, subtraktion, multiplikation og division, men giver også praktiske tips og tricks til at gøre det lettere at håndtere disse typer af beregninger.

Skriftlig addition
Skriftlig addition bør være en del af generel matematisk viden. Det er processen med at lægge to eller flere tal sammen ved at skrive dem under hinanden og lægge dem sammen fra højre mod venstre, dvs. fra et-tallerne til de højere cifre. Få matematik hjælp til dit barn eller til dig selv, hvis du gerne vil blive bedre til faget.
Summen skrives derefter under bindestregen på samme sted. Det gør det nemt at lægge store tal sammen trin for trin.
Tilføjelse i skrift med mente
Men hvad sker der, hvis det tal, du skal skrive under skråstregen, har mere end ét ciffer? Hvis summen af cifrene er større end ni, skal der lægges en 'i mente' til det næste ciffer til venstre. For eksempel når man lægger 467 og 589 sammen: Man lægger først enerne sammen (7+9=16), skriver 6 under enerne og fører 1 over til tierne, hvor 6, 8 og den overførte 1 så lægges sammen (15), og så videre. Du kan finde hjælp til matematik online på Superprof, så du kan komme tættere på dine professionelle mål!
Skriftlig addition med decimaltegn / decimaltal
Når man lægger decimaltal sammen, er det vigtigt at placere kommaerne præcis under hinanden. For eksempel: 47,5 + 3,75. Juster tallene, så decimalerne passer sammen, og adder som normalt, idet du placerer decimaltegnet lige under decimaltegnet i summen.
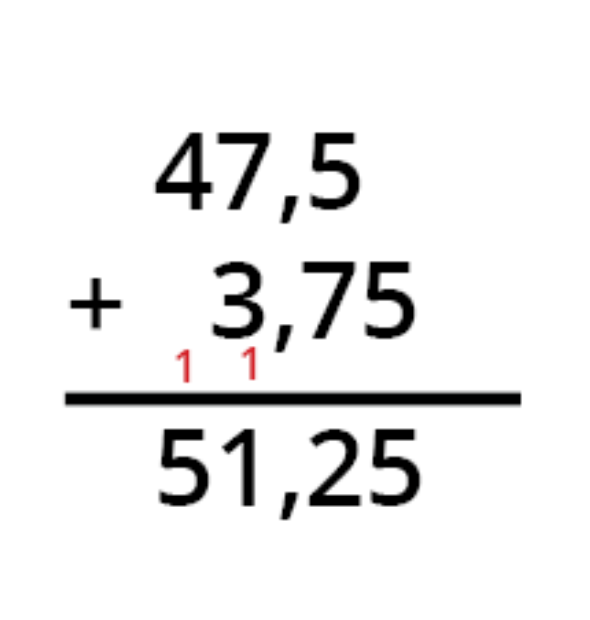
For eksempel: 47,5 + 3,75. Juster tallene, så decimalerne passer sammen, og læg dem sammen som sædvanligt, idet du placerer decimaltegnet direkte under decimaltegnet i summen. Så fra højre mod venstre skal du beregne 0+5=5, 7+5=12 (dvs. skriv 2 og overfør 1'eren), derefter kommer komma, 7+3+1=11 (igen skriv 1 og overfør 1) og 4+1=5. Resultatet fra 47,5+3,75=51,25.
Med nogle få øvelser og tekstopgaver vil skriftlig addition, uanset om det er med decimaltegn eller udregninger med store tal, snart være meget let for dig.
Subtrahere skriftligt
Skriftlig subtraktion er en grundlæggende matematisk færdighed, som gør det muligt at trække et tal fra et andet ved at skrive dem under hinanden og subtrahere dem fra hinanden. Dette introduceres i folkeskolen og er afgørende for at forstå mere avancerede matematiske begreber.
Ligesom ved addition går man fra højre mod venstre og trækker det nederste tal fra det øverste. For 1785-562 går man frem på følgende måde: 5-2=3, 8-6=2, 7-5=2, 1-0=1. 1785-562=1223.
Skriftlig subtraktion
Subtraktion med overførelse opstår, når cifret i det tal, der skal trækkes fra (subtrahend), på et tidspunkt er større end det tilsvarende ciffer i det tal, der skal trækkes fra (minuend). For at løse denne situation "låner" man en tierenhed fra det næsthøjeste tal i minuenden. Denne tierenhed lægges til det nederste cifers minuend, og det øverste cifers minuend reduceres med én. Du kan finde matematik b kursus Århus, så du styrke dine kundskaber i faget!
Addition: Summand+Summand=Sum
Subtraktion: Minuend-Subtrahend=Difference
Multiplikation: Factor x Factor=Product
Division: Dividend/Divisor=Quotient
Lad os tage subtraktionen 705 - 387 som et eksempel. Vi starter med enerne: 5 er mindre end 7, så du låner en tier fra tierne (0), hvilket gør dette tal til -1. For at kompensere for dette lægger du 10 til enerne, hvilket gør 5 til 15. Nu kan du trække 7 fra 15, hvilket giver 8.
Du har nu -1 for tierne, hvilket betyder, at du låner endnu en tierenhed fra hundrederne (7). Det reducerer 7 til 6, og tierne bliver til 9. Nu trækker du 8 fra 9, hvilket giver 1. For hundredtallet skal du blot trække 3 fra 6, hvilket giver 3. Det endelige resultat er 318.
Skriftlig subtraktion med decimaltal
Når man subtraherer decimaltal, også kendt som decimaltegn, er det lige så vigtigt som ved addition at placere kommaerne nøjagtigt under hinanden for at sikre den korrekte placering af decimalerne.
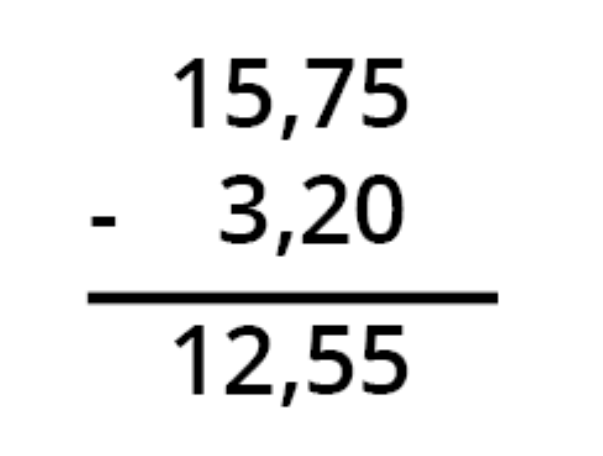
For eksempel: 15,75 - 3,2 justeres til 15,75 - 3,20, før subtraktionen udføres.
Begynd at trække fra højre mod venstre med decimaltegnet i løsningen nøjagtigt under de andre decimaltegn.
Skriftlig subtraktion: Subtraktionsmetode / additionsmetode
I den klassiske subtraktionsmetode trækkes hvert ciffer i det nederste tal fra det tilsvarende ciffer i det øverste tal. Hvis et tal er mindre end det nederste, er det nødvendigt at overføre det. Med suppleringsmetoden bestemmer du derimod hvilken værdi, der skal lægges til det nederste tal for at nå det øverste tal. Dette kan forenkle opgaven og er især nyttigt for mere komplekse tal.
Opdeling på skrift
Skriftlig division er en vigtig matematisk færdighed, der giver dig mulighed for at dividere et tal med et andet for at bestemme et resultat og, om nødvendigt, en rest. Denne færdighed bruges også ofte i matematiktest i faktuelle opgaver. Skriftlig division foregår i tre trin.
- Divider det første ciffer fra venstre i det venstre tal (dividenden) med det højre tal (divisoren).
- Multiplicer delresultatet med divisoren, skriv et minustegn under det venstre tal
- Skriftlig subtraktion

Hvis vi for eksempel har opgaven 853:4, starter vi med trin 1 og udregner 8:4=2. 2 er derfor vores første delresultat, som vi skriver efter =. Nu fortsætter vi med trin 2 og udregner vores delresultat divideret med divisoren, dvs. 2*4=8. Vi skriver nu 8 med et minus under det første tal fra venstre for vores dividende, og så er vi allerede ved trin 3, subtraktionen. 8-8=0.
Nu tager vi det næste ciffer i vores division (dvs. 5'eren) og starter igen fra begyndelsen.
Først skriver vi 5 ved siden af resultatet af vores subtraktion fra før, dvs. ved siden af 0. Så starter vi igen med trin 1: 5 divideret med 4 er 1, da 4 kun passer ind i 5 én gang.
Så 1 er vores næste divisor og går ved siden af den 2'er, vi lige har skrevet. 1*4=4 og så skriver vi 4'eren med et minus under 5'eren og fortsætter med subtraktionen. 5-4=1 og vi skriver 1 nederst og trækker det sidste ciffer i vores dividende (3) med ned.
Da vi nu er nået til det sidste ciffer i dividenden, skal vi nu regne med alt under linjen. Så med 13. 13:4=3, er 3'eren vores sidste delresultat. 3*4=12, vi skriver 12 med et minus under 13, så vi har 1 tilbage. Dette er vores rest. Vi skriver den simpelthen med dit R foran efter vores resultat. Dette giver løsningen fra 853:4=213R1.
Skriftlig division med decimaltegn / decimaltal
Når man dividerer decimaltal, placeres decimaltegnet i kvotienten direkte over decimaltegnet i dividenden, så snart dividenden er blevet divideret helt. Hvis det er nødvendigt, kan dividenden udvides ved at tilføje nuller for at fuldføre divisionen. Eksempel: 12,4 divideret med 2 resulterer i 6,2.
Skriftlig division med store tal
Division af store tal følger samme procedure, men kræver flere trin og mere præcision. Det er nyttigt at dele tallene op i mindre, overskuelige segmenter og trække divisoren fra det største ciffer i dividenden trin for trin.
Skriftlig multiplikation
Skriftlig multiplikation er en grundlæggende metode i matematik, som gør det muligt for eleverne at gange store tal ved at lægge dem sammen trin for trin. Denne færdighed er meget vigtig, for eksempel når man omregner måleenheder.
Multiplikation på skrift
Når du skal gange skriftligt, skal du først skrive udregningen ned. Tallet til venstre er multiplikatoren, og tallet til højre er multiplikanden. Du starter med at gange multiplikatoren med multiplikandens forreste tal. Du trækker en streg under hele opgaven og skriver dette delresultat nedenunder. Fortsæt på denne måde med de andre cifre i multiplikanden. Til sidst lægger du alle de enkelte resultater sammen for at få det endelige resultat.
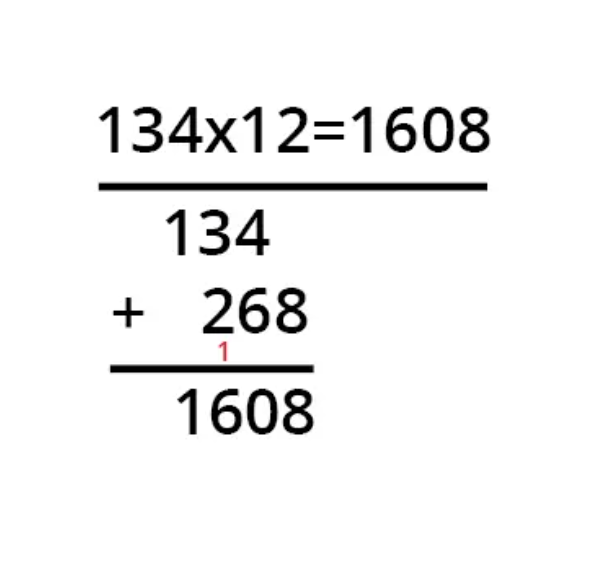
Så hvis du nu vil beregne 134*12, beregner du først 1*134. Dette resulterer i 134. Du trækker en streg under problemet og skriver dette delresultat ned, så det sidste ciffer (dvs. 4'eren) står præcis under multiplikandens første ciffer. Fortsæt derefter og beregn 134*2=268. Skriv nu 268 en plads til højre under delresultatet af (134). Tilføj derefter skrivningen og kom frem til 1608. 134*12=1608.
Skriftlig matematik i form af multiplikation med decimaltegn
Når du multiplicerer decimaltal, skal du først flytte så mange cifre til højre, at der ikke er flere kommaer i cifrene. Når du har udført multiplikationen som beskrevet ovenfor, skal du sætte decimaltegnet i resultatet, så antallet af decimaler svarer til summen af decimalerne i de to oprindelige tal. For eksempel: 12,3 ganget med 3,4 resulterer i 41,82, da begge tal tilsammen har to decimaler.
Sammenfat med AI















