I dag skal vi se på opløsning af kræfter. Det er et emne, du vil støde på i et matematikmodul i mekanik, og det kan være svært at finde rundt i i starten. For at komme i gang repeterer vi nogle af de kernebegreber, som vi skal være fortrolige med, før vi går videre til nogle sværere problemer.
Før du går videre, skal du sørge for, at din matematiske viden omfatter en god forståelse af algebra.
Tyngdekraft
Det er ret vigtigt at huske et par vigtige fakta om tyngdekraften. Vi siger normalt, at tyngdekraftens acceleration er 9,8ms^-2. Sådan er det på jorden, og ofte erstattes dette tal bare af symbolet "g".
Vi bliver også nødt til at kende til kræfter. Fra fysikken kan du måske huske, at F = ma. Det vil sige, at en kraft (i Newton) er lig med et objekts masse ganget med dets acceleration.
Vi har lige antydet, at tyngdekraften i virkeligheden bare er en acceleration. Med det i tankerne kan vi justere vores ligning ovenfor en smule for at lave denne nye: W = mg
Det vil sige, at vægten er lig med massen af en genstand ganget med tyngdeaccelerationen. Du kan sikkert bruge dine matematiske evner til at se, at det algebraisk set er den samme ligning, bare med en specifik acceleration (tyngdekraften). Det betyder også, at vægt er en kraft.
Trigonometri
Der er en sidste ting, du skal have styr på, før vi går i gang, og det er vores grundlæggende trigonometriske funktioner: SOHCAHTOA.
Vi får brug for dem, fordi opløsningen af kræfter indebærer, at hver kraft opdeles i en x (vandret) og en y (lodret) komponent, men mere om det nedenfor.
Er du også nysgerrig på at blive klogere på hvordan infinitesimalregning fungerer?
Opløsning af kræfter
Lad os komme i gang med at løse nogle kræfter! Vores spørgsmål vil være teoretisk, da vi ikke ønsker at komplicere det for meget, men ofte vil du se, at disse spørgsmål involverer en eller anden form for scenarie, og nøglen er at koge det ned til et sæt tal, som du kan løse.
Husk: tegn altid et diagram!
Lad os sige, at der er to kræfter, der virker på et objekt. Den ene kraft virker vandret med en størrelse på 50 N, mens den anden kraft virker i en vinkel på 20 grader med en størrelse på 20 N. Hvad er den resulterende ("samlede") kraft, der virker på dette objekt?
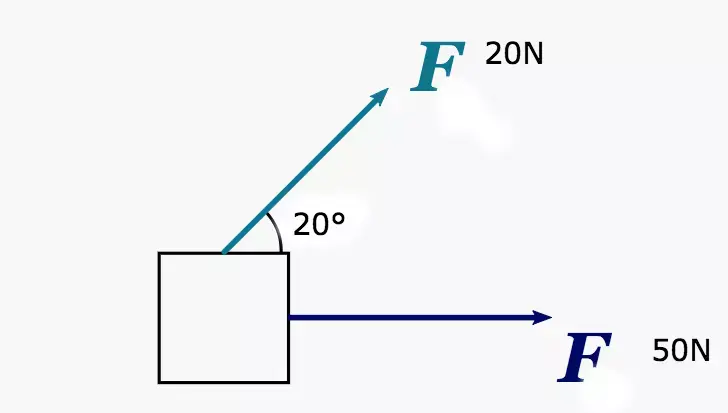
Fordi disse to kræfter virker i forskellige retninger, kan vi ikke bare lægge dem sammen og få den resulterende kraft. Husk, at "resultant" bare er et finere ord for at sige samlet eller total.
Vores kraft på 50N virker kun i én retning (vandret), så der er ikke så meget at gøre her. Vi vil fokusere på kraften på 20N, der virker i en vinkel på 20 grader. Ligesom jeg nævnte før, skal vi opdele denne kraft i dens komponenter (dvs. den mængde, der virker vandret (på x-aksen), og den mængde, der virker lodret (på y-aksen)). Bare rolig, det er ikke så svært!
Hvis vi forestiller os vores 20N-kraft, der virker ved 20 grader, som en trekant, så har vi en retvinklet trekant - med en spids vinkel på 20 grader. Hypotenusen i trekanten ville være 20N.
Ved hjælp af SOHCAHTOA og lidt simpel algebra kan vi beregne de kræfter, der virker på vores tilstødende og modsatte trekantsider. Vi starter med at beregne den vandrette kraft, som virker på x-aksen, og som er den tilstødende side i vores trekant.
Brug af SOHCAHTOA:
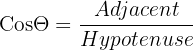
Vi ved, at vores vinkel er 20, og at hypotenusen også er 20. Med lidt omrokering kan vi omarrangere denne ligning for at finde størrelsen af vores kraft i vandret retning:
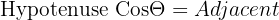
Og hvis vi sætter vores tal ind:
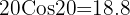
Vores kraft virker med 18,8 Newton i vandret retning.
For at finde ud af, hvor stor en kraft der virker i den lodrette retning, kan vi lave en meget lignende beregning, hvor vi bare bruger sin i stedet for cos.
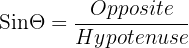
Igen kan vi bruge vores viden om algebra til at omarrangere denne ligning, men denne gang skal vi finde den modsatte side af trekanten. Den modsatte side er den side, der er lodret, og repræsenterer vores krafts størrelse på y-aksen.
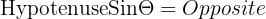
Igen har vi allerede vores vinkel (som theta repræsenterer) og hypotenusen, så vi kan bare sætte dem ind for at finde den kraft, der virker lodret:
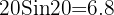
Fedt! Den kraft, der virker lodret fra vores oprindelige 20N-kraft i en vinkel på 20 grader, er 6,8N!
Vil du også gerne blive bedre til at løse matematiske opgaver i differential- og integralregning?
At sætte det hele sammen
Så på dette tidspunkt ved vi, at der var en kraft på 50N, der virkede vandret på vores objekt, og en kraft på 20N, der virkede i en 20-graders vinkel. Vi har lige delt den 20N kraft op i en 6,8N lodret kraft og en 18,8N lodret kraft.
For at finde vores resulterende kraft skal vi bare lægge disse værdier sammen.
Lodrette kræfter
Vi starter med de lodrette kræfter. Det bliver ret nemt:
6,8N + 0 = 6,8N
Jep, det er rigtigt: Vores vandrette kraft på 50 N virker slet ikke i den lodrette retning, så kraftmængden der er 0. Det efterlader os bare med den lodrette komponent af vores kraft på 20 N.
Vandrette kræfter
Den her bliver lidt mere kompleks, men stadig ret intuitiv:
50N + 18,8N = 68,8N
Vi tager vores vandrette kraft på 50N og lægger den til den vandrette del af kraften på 20N. Det efterlader os med en samlet kraft på 68,8 N på X-aksen.
En endelig trekant
Så vi har nu de to komponenter af vores resulterende kraft, men ikke den samlede kraft. Det vil sige, at vi kender den resulterende kraft vandret og den resulterende kraft lodret, men vi ved ikke, hvad de er tilsammen. For at løse dette kan vi bruge en sidste trekant.
Placer din vandrette kraft på 68,8 N på den tilstødende side af trekanten og din lodrette kraft på 6,8 N på den modsatte side af trekanten.
Hvordan kan vi beregne den kombinerede kraft? Ved hjælp af vores trofaste trekantsligning... Pythagoras' læresætning! Vi har to sider i trekanten, og at beregne hypotenusen er bare et spørgsmål om:
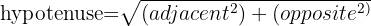
Lad os indsætte vores værdier og afslutte med at løse den samlede resulterende kraft:
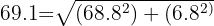
Og der har vi det: en resulterende kraft på 69,1 N.
Lidt ekstra
Et sidste spørgsmål, du måske bliver stillet, er at løse vinklen på den resulterende kraft. Nu hvor vi har alle tre sider af trekanten, er det nemt med SOHCAHTOA.
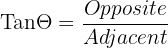
For at finde vinklen skal vi bare bruge den inverse tan-funktion.
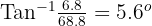
Og der har vi det: Vores resulterende kraft virker i en vinkel på 5,6 grader.
Opsummering
Vi håber, at du fandt denne artikel informativ. Vi vil anbefale, at du fortsætter med at studere ved at bruge nogle tidligere eksamensspørgsmål eller regneark, der præsenterer dette problem, som vi har gjort ovenfor, og derefter nogle, der bruger et scenarie som at beregne de kræfter, der virker på en billedramme.
Husk: Repetition er nøglen til at få succes til matematikeksamen! Når du først har forstået principperne, er hvert spørgsmål det samme, fordi læseplanen kun angiver bestemte emner, der skal studeres.
Det er vigtigt at bemærke, at vi ikke har taget højde for friktion i dette eksempel, men det kan komme på tale til en eksamen. Hvis du føler, at du har brug for mere hjælp til at løse kræfter som en del af dit mekanikarbejde, vil vi anbefale, at du finder en matematiklærer på Superprof, som kan hjælpe dig med at studere!
At bruge matematiklærere hjælper dig med at forstå matematiske begreber som logaritmer, algebra, differentialregning og meget mere, som du måske ikke har forstået i klasseværelset, og gør det muligt at undervise i emner på en måde, der passer til dig.
Kunne du lide denne artikel? Skriv en anmeldelse!
Loading...
