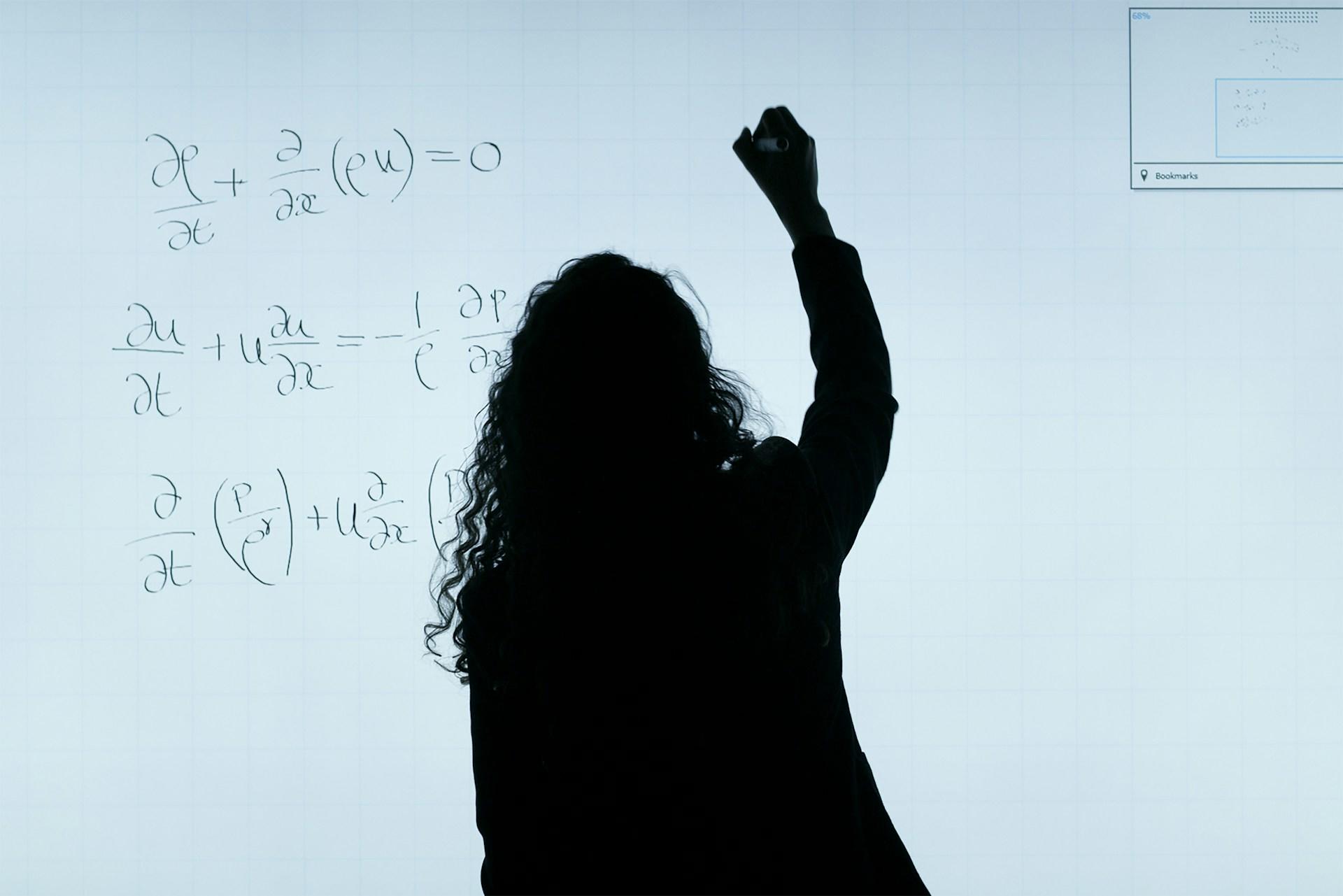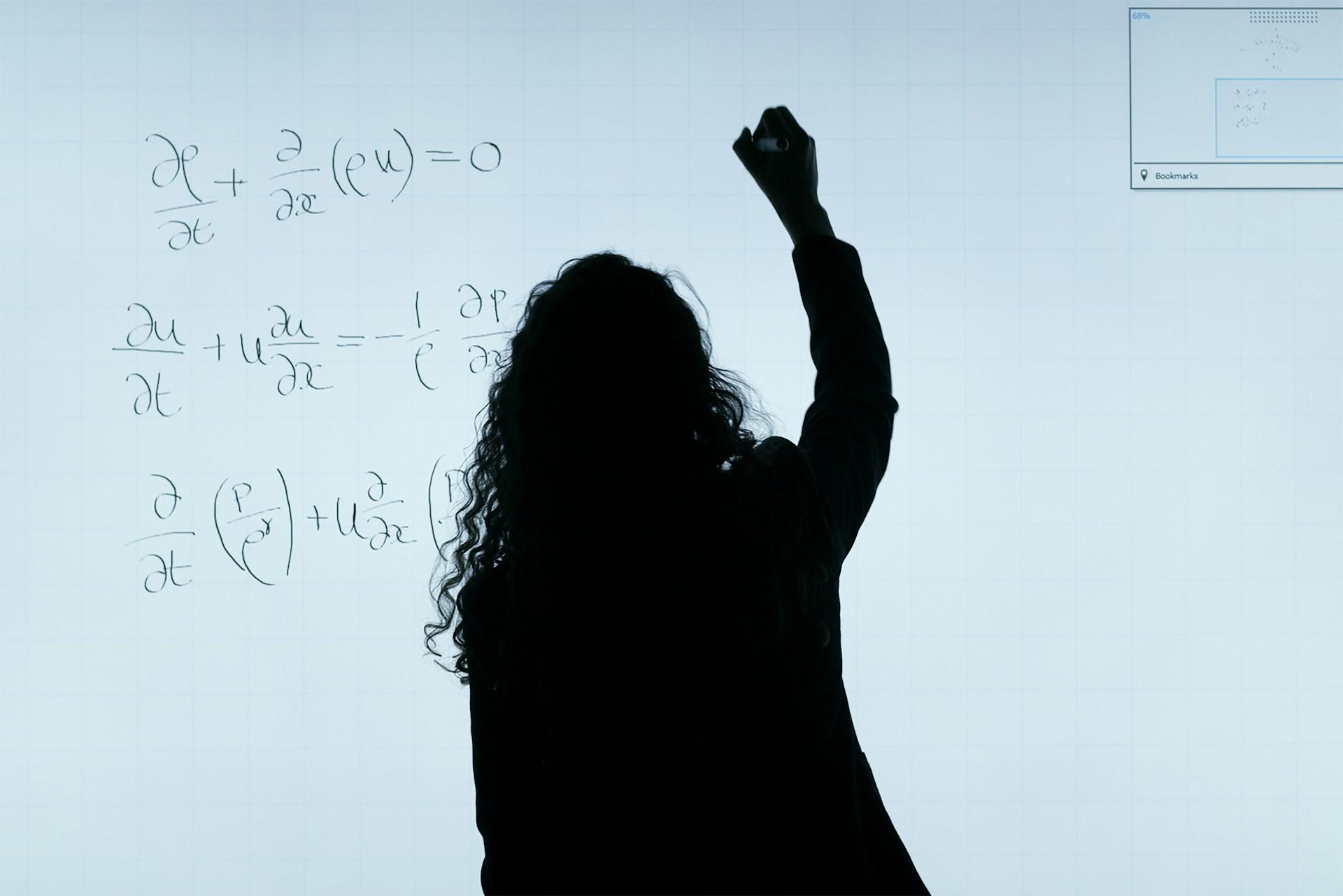Dansk matematikundervisning har længe set ens ud. Samtidig får bestræbelserne på at forbedre læringsresultaterne for elever i alle aldre flere og flere til at se sig om i verden for at se, hvilke metoder vi kan udvikle. En af disse metoder er Singapore-modellen.
Singapore matematik (internationalt kendt som Singapore Maths) blev født ud af et behov for en læseplan i et helt nyt land og blev designet til at fremme børns problemløsningsevner, kritiske tænkning og logiske tilgange. En pædagogisk metode, der visualiserer og konkretiserer det abstrakte i matematikken.
Lyder det kompliceret? Lad os forklare det lidt tydeligere.
Hvad er Singapore-modellen?
Singapore-modellen lærer eleverne matematik ved at forbinde abstrakte matematiske begreber som ligninger, brøker og procenter med konkrete og visuelle midler. Selve metoden er baseret på tre faser, kendt som CPA-metoden, som arbejder parallelt for at hjælpe eleverne med at visualisere og løse matematiske problemer.
Men ud over metodens tilgang anses Singapore matematik også for at hjælpe børn med at styrke deres evner til problemløsning og logisk tænkning samt øge deres selvtillid, hvilket igen fører til et positivt forhold til faget.
Hvordan blev Singapore-metoden skabt?
Singapore-modellen blev faktisk udviklet, fordi Singapore blev uafhængig af Malaysia i 1965 og ikke havde noget system for økonomi, politik, uddannelse og så videre. Som følge heraf udviklede Singapores undervisningsministerium en helt ny læseplan baseret på forskning fra tre fremtrædende matematikere og undervisere fra 1960'erne og 1970'erne.
Det er disse tre undersøgelser, der ligger til grund for metoden, som fokuserer på blokke, CPA-tilgangen og stræben efter at give eleverne et godt forhold til matematik. Metoden blev lanceret og implementeret i 1992 og har siden bidraget til, at Singapores elever er blandt verdens bedste til matematik i alle tests.
Du har måske svært ved at se forskellen mellem dette og almindelig matematikundervisning. Andre ser forbindelser mellem Singapore-matematik og Montessori-metoden. Så lad os afklare begreberne.
Forskellene mellem Singapore-metoden, Montessori og traditionel matematikundervisning
Hvis vi starter med at sammenligne Singapore-metoden med Montessori-metoden, er der både ligheder og forskelle. En af de største forskelle mellem de to metoder er deres hensigt. Montessori-metoden er en metode til at lære at lære. Den fremmer disciplin og uafhængighed, to forhold, som Singapore-metoden ikke tager højde for. Fagspecifik træning, og hvordan man underviser i begreber, er to andre ting, der adskiller de to systemer;
Desuden fremmer Montessori-metoden individuel opdagelse. Med Singapore-metoden arbejder hele klasseværelset med at anvende blokmodeller på specifikke problemer samtidig. Montessori-metoden lægger vægt på, at eleverne arbejder med så lidt lærervejledning som muligt.
Men begge metoder involverer læring gennem manipulation og verbalt udtryk af koncepter, og begge tilskynder til kritisk tænkning og problemløsning.
Når det kommer til at sammenligne Singapore-matematik med traditionel matematikundervisning, er der mange flere forskelle.
Traditionel matematikundervisning
- Underviser overfladisk i mange områder
- Rutinemæssig gentagelse, indtil informationen er lagret i hukommelsen.
- Der undervises i koncepter efter niveau.
- Abstrakte præsentationer
- Fokus på at huske
Singapore-metoden
- Undervis i færre områder, men mere dybdegående.
- Internalisering, ikke memorering
- Begreberne læres i rækkefølge
- Praktiske øvelser
- Fokus på problemløsning
Nu har vi fået en bedre forståelse af, hvad Singapore-metoden er som helhed. Lad os se nærmere på, hvordan den fungerer i praksis.
Hvad er CPA-metoden?
Matematik er et abstrakt begreb. For at forstå det må vi først definere, hvad det repræsenterer og kan udrette. Vi bruger symboler til at angive matematiske funktioner og tal til at vise værdi. Ved at give os selv visuelle ledetråde gør vi det muligt at udforske det, vi ikke kan se eller røre ved.
Concrete (Konkret): håndtering af fysiske objekter for at skabe interaktion med former og begreber.
Picturial (Billedlig): give problemer en visuel repræsentation for at finde løsninger.
Abstract (Abstrakt): omdanne indlærte begreber til matematiske færdigheder.
Brug af CPA-tilgangen hjælper eleverne med at forstå matematik.
Den konkrete fase
Det er på dette stadie, at børnene afprøver og lærer grundlæggende matematiske begreber ved at håndtere virkelige objekter. I denne fase bør læreren udfordre eleverne til at "forklare matematikken". Ved verbalt at udtrykke, hvad deres fysiske handlinger repræsenterer, lærer de at fastslå, hvad de netop har lært.
For eksempel kan vi evaluere et aritmetisk matematikproblem, der involverer at lægge stykker slik sammen. Først skal eleven have to bunker slikstykker, der repræsenterer de numeriske værdier, der er angivet i problemet.
De skal så løse problemet ved at sidde sammen og tælle godbidderne. At forklare matematikken kan lyde nogenlunde sådan her:
- Jeg har fire stykker slik;
- Giv mig tre stykker slik mere;
- Nu har jeg (tæller) syv stykker slik!
- Fire bolsjer plus tre bolsjer giver syv bolsjer;
Ud fra dette perspektiv kunne man tro, at Singapore-metoden er en bogstavelig øvelse. De problemer, der præsenteres i matematikbogen, kommer til live i klasseværelset.
Den billedlige fase
Denne fase er en anden form for informationsmanipulation, selv om den er mere subtil end den foregående. Eleverne lærer at konvertere de tidligere brugte fysiske objekter til visuelle billeder. I denne fase vil de udforske, hvad blokmodeller er, og hvordan de kan bruge dem til at løse deres opgaver.
Denne læringsfase hjælper eleverne med at omfavne, øve og udtrykke abstrakt matematisk tænkning. Den fremmer elevernes problemløsningsevner, da de skal finde ud af, hvordan de omdanner konkrete repræsentationer til semi-abstrakte visuelle billeder, som f.eks.
- Numeriske linjer
- En lige linje
- En visuel repræsentation
- Tal arrangeret i rækkefølge efter deres værdi
- Grafer
- Blokdiagrammer
- Billedgrafer
- Linjegrafer
- Blokmodeller
- For at identificere tendenser og mønstre
- For at se sammenhænge mellem forskellige datasæt
Den abstrakte fase
På den rigtige måde, starter den abstrakte fase næsten automatisk. Eleverne beslutter, at de simpelthen ikke længere har brug for at repræsentere problemet foran dem manuelt eller visuelt. De har skabt en forbindelse mellem "tænkende" matematik og den virkelige verden.
Eleverne kan nu ræsonnere sig gennem matematiske opgaver uden opfordring og med meget lidt vejledning. De kan bruge ord og symboler til at udtrykke sig matematisk. De er også trygge ved at arbejde med de begreber, man har introduceret dem til.
På dette stadie kan eleven relatere begreberne til andre matematiske begreber, de kender, og er klar til at lære mere.
Hvad er blokmodeller?
Blokmetoden er et system, der gør matematikken synlig og relaterbar.
Den hjælper elever med at udvikle et godt forhold til matematik.
Blokmetoden hjælper børn med at forstå forholdet mellem matematik og virkelighed.
Metoden lærer børn at udvikle en talforståelse og forbedre deres problemløsningsevner.
En rigtig god anvendelse af blokmodeller er, når læseforståelsen kommer i spil. Ofte skaber denne type matematikopgaver stor forvirring hos eleverne, fordi vigtige oplysninger er skjult i fakta, som hverken er relevante eller nyttige. For at kunne modellere læsesnak skal eleven identificere relevant information i læsesnakken og derefter illustrere blokke, der repræsenterer informationen.
Der er således flere anvendelsesmuligheder for blokmodellerne som:
- At organisere information
- At repræsentere matematiske problemer visuelt
- At vurdere svarene på matematikopgaver
- At afgøre, hvilken beregningsmetode der vil løse problemet
- At opløse læsetal
Denne oversigt over Singapore-metodens blokmodeller baner vejen for, at eleverne kan forstå og arbejde med abstrakte matematiske problemer. Det opmuntrer dem også til at tænke logisk i stedet for kun at løse matematiske problemer i deres hverdag.
Sådan bruger du blokmodeller i praksis
At lære matematik med den effektive Singapore-metode revolutionerer den måde, vi laver matematik på. Den lærer eleverne forskellige metoder til problemløsning. En af disse er blokmodellen. Men hvordan arbejder man med blokmodeller i praksis? Lad os se på nogle eksempler.
Til at begynde med kan blokmodeller bruges til forskellige typer af problemer.
- Grundlæggende aritmetik - addition, subtraktion, multiplikation og division;
- Løse brøker
- Beregne procentpoint
- Løse læsetal
Dem vil vi se nærmere på.
Løs enkle additionsopgaver med blokmodellen
Nøglen til korrekt blokmodellering er at opstille alle de oplysninger, som matematikopgaven giver dig. Matematikopgaver kan give dig forskellige værdier, og du skal finde de ukendte størrelser. En opgave i addition kan se sådan ud: 4+9=?
Sådan en ligning er alt for simpel, selv for folkeskoleelever. På det niveau arbejder eleverne med læsetaler, så lad os gentage den samme ligning. Men denne gang som en tekst:
Sandra og Louise plukker blomster på en eng. Sandra plukker fire blomster, og Louise plukker nine blomster. Hvor mange blomster har pigerne plukket i alt?
- Trin 1: Fremhæv vigtige oplysninger (som ovenfor)
- Trin 2: Modellering af information: Sandra 🌸🌸🌸🌸, Louise 🌸🌸🌸🌸🌸🌸🌸🌸🌸
- Trin 3: Tæl alle blomsterne
- Trin 4: Fortæl os om dit resultat. Skriv det derefter ned.
Addition i blokmodellen hjælper vores yngste elever med at 'se' deres matematiske tal og forstå, hvordan det fungerer. Den visuelle repræsentation lægger grunden til, at eleven kan bygge videre på sine færdigheder.
Multiplicer ved hjælp af blokmodellen
Du tænker måske, at en række blomster slet ikke er en blok, og det har du helt ret i. Ikke desto mindre er det sådan, blokmodellen er en god start for de alleryngste elever. I løbet af årene vil eleverne udvikle sig til mere komplekse og abstrakte repræsentationer. De kan f.eks. tegne cirkler for at illustrere mængder og senere gå videre til rektangler.
Med tiden vil eleverne lære at tegne rektangler for at repræsentere Sandra og Louise. De vil også skrive tal i stedet for at tegne figurer i en kasse. Det bliver starten på deres rejse ind i den abstrakte matematik.
Når eleverne starter med multiplikation, er de fortrolige med at arbejde med blokmodellen for at løse problemer. Denne fortrolighed gør det lettere for dem at sætte sig ind i multiplikations- og divisionsøvelser.
Jacob køber tre æsker med slik. Hver æske indeholder seks stykker slik. Hvor mange stykker slik har Jacob købt?
For at modellere dette matematiske problem starter vi med at fremhæve mængderne, som du kan se ovenfor. Dernæst modellerer vi vores problem:
- Tegn et stort rektangel for at repræsentere det samlede antal stykker slik, den ukendte værdi;
- Tegn to lodrette linjer, så rektanglet får tre felter (sørg for, at felterne har samme størrelse);
- Skriv tallet 6 i hver kasse;
Det gør ligningen mere visuel. Eleven kan enten skrive tallet 6 i æsken eller blot tegne seks stykker slik i hver æske. Uanset hvad hjælper det os med at illustrere det samlede antal stykker slik, som Jacob har købt.
Visualisering af læsning ved hjælp af blokmodellen
Vi slutter af med en læsetale, der er lidt mere kompleks end dem, vi har set på tidligere. Denne type læsetale udfordrer selv de mest erfarne matematikstuderende.
En krukke består af 301 glaskugler, som alle har en af farverne rød, grøn eller blå. I glasset finder vi dobbelt så mange blå kugler som grønne. Og dobbelt så mange røde kugler som blå. Hvor mange kugler er røde?
Blokmodellen til denne matematikopgave ser lidt anderledes ud end dem, vi har løst før. Den har tre blokke, en for hver farve marmor. I stedet for en blok med tre dele.
- Den første blok er et simpelt rektangel, som skal repræsentere farven grøn;
- Den anden blok er et rektangel med to dele, fordi vi har dobbelt så mange blå kugler som grønne;
- Den tredje blok er et rektangel med fire dele, fordi vi har dobbelt så mange røde kugler som blå;
- Vores model præsenterer os for syv rektangler.
- Det samlede antal kugler er 301;
Denne tredelte blokmodel giver os mulighed for at beregne værdien i hver trekant. Det er en enkel opgave, da vi kender antallet af rektangler og det samlede antal kugler;
Ligningen er 301÷7 = ? Svaret er 43. Det fortæller os, at der er 43 grønne kugler i glasset. For at finde ud af, hvor mange blå kugler vi har, skal vi gange 43 med to (43 x 2) og få svaret 86 blå kugler i glasset. Derefter ganger vi 43 med fire for at finde ud af antallet af røde kugler, 43 x 4 = 172. Selv om vi nu har svaret, er der i alt 172 røde kugler, men det kan være klogt at tjekke antallet. 43+86+172 = 301. Det er korrekt!
Som du kan se, anvendes blokmodellen på flere forskellige typer af matematiske problemer. Og det er bare et udsnit. Der er uendeligt mange problemer, som blokmodellen hjælper med at visualisere og løse. Med andre ord lærer eleverne, hvordan de kan arbejde med et problem for at gøre det visuelt og mere håndgribeligt.
Kunne du lide denne artikel? Skriv en anmeldelse!
Loading...
